De los números primos a los algoritmos

Introducción

Históricamente, en las matemáticas las preguntas solían ser sobre igualdades entre valores, o sobre la veracidad de ciertas afirmaciones. Algunos ejemplos:

¿Es la hipotenusa al cuadrado la suma de los catetos al cuadrado?
¿Existen infinitos números primos?
¿Existe alguna solución con números enteros a la ecuación $a^3 = b^3 + c^3?$
¿Se puede colorear siempre cualquier mapa con tan solo cuatro colores, de manera que las regiones adyacentes no compartan color?

Sin embargo, el planteamiento de otra clase de preguntas fue abriendo poco a poco otro mundo dentro de las matemáticas: el mundo de los algoritmos.

Los números primos

Definición: Decimos que un número entero $P$ es primo cuando solo tiene dos divisores: $1$ y $P.$
Otra forma de verlo es que no se pueden factorizar como el producto de dos enteros distintos de $1$.

Por ejemplo, $5$ solo se puede factorizar como $1\times5$, por lo que es primo. Sin embargo, $21$ se puede factorizar como $3\times7$, por lo que no lo es.

La infinitud de los números primos

Existen infinitos números primos, y podremos deducirlo si primero tenemos en cuenta la proposición a continuación.

Proposición: Para cualquier entero $N$, se cumple que $N$ y $N+1$ no tienen divisores en común (excepto $1$).
Demostración: Un número $K > 1$ tiene múltiplos $K, 2K, 3K, 4K \dots$ La diferencia de dos múltiplos siempre es otro múltiplo, y en concreto, al menos $K$. Si $N$ es múltiplo de $K$, el siguente múltiplo es $N+K$ y, por tanto, $N+1$ no lo sería. Con esto vemos que nunca se va a dar el caso que ambos sean múltiplos de $K > 1$ y por tanto su único divisor común es $1$. $\hspace{1em} \blacksquare \hspace{1em}$ (el cuadrado denota el fin de la demostración)

Una vez visto esto, vamos a demostrar por contradicción que existen infinitos números primos. La idea es que vamos a asumir lo contrario, que hay un número finito, como cierto. Luego, razonaremos hasta llegar a algo absurdo, y por tanto la explicación de este absurdo es que nuestro punto de partida no era cierto, y por eso llegamos a contradicciones.

Definición: $N!$ es el factorial de $N$, y se trata del producto de todos los números entre $1$ y $N$, es decir,

\[N! = 1 \times 2 \times 3 \times \dots \times (N-1) \times N\]

Por ejemplo, $4! = 1\times 2 \times 3 \times 4 = 24.$

Teorema de Euclides: Existen infinitos números primos.
Demostración: Supongamos que hay una cantidad finita de números primos. Entonces existe un último número primo, el mayor de ellos, que lo podemos llamar $P_{\max}$. Consideremos el siguiente número:

\[M := P_{\max}! = 1\times2\times3\times4 \times \dots \times (P_{\max}-1) \times P_{\max}\]

($:=$ denota que se trata de una definición)
Se trata del producto de todos los números entre $1$ y $P_{\max}.$ Sin duda es un múltiplo de todos los números desde $1$ hasta $P_{\max},$ y por tanto es múltiplo de todos los primos.

Si ahora nos preguntamos qué pasa con $M+1$ llegamos a un resultado muy interesante. Como hemos visto antes, $M$ y $M+1$ no tienen divisores comunes excepto el $1$, pero $M$ era divisible entre todos los primos, por lo que $M+1$ no es divisible entre ningún primo! Es decir, que $M+1$ solo tiene divisores $1$ y $M+1$. Esto nos dice que $M+1$ es primo, pero habíamos dicho que el mayor primo era $P_{\max}$, pero $M+1$ es mucho mayor… No tiene ningún sentido. Tenemos delante una contradicción, lo que nos dice que nuestra suposición era falsa y no puede haber una cantidad finita de números primos. Si no pueden ser finitos, ¡solo pueden ser infinitos! $\hspace{1em} \blacksquare$

Otras preguntas interesantes sobre los números primos

Una vez que sabemos que existen infinitos primos, parece que ya no es muy interesante buscar nuevos primos. Al fin y al cabo, si queremos encontrar primos, solo tendríamos que ir probando números y mirar si son divisibles entre números más pequeños, y siempre encontraremos un nuevo número primo.

Pero en realidad quedan muchas preguntas interesantes:

¿Cada cuántos números hay un número primo?
¿Por qué cada vez hay más distancia entre un número primo y el siguiente?
¿Cómo podemos saber si un número enormemente grande es primo, si probar todos los posibles divisores no es factible?
¿Cómo podemos encontrar todos los primos hasta un cierto valor de manera rápida?

Las dos primeras preguntas resultan bastante complicadas, tanto que requerirían su propia entrada en el blog. En esta entrada nos centraremos en la última.

Buscando números primos

Si nos preguntamos cómo encontrar primos entre $1$ y $N$ de manera rápida, primero deberíamos poder medir qué tan rápido es un cierto método. Más adelante definiremos estos conceptos de una forma más rigurosa, pero por ahora podríamos decir que, como cada vez que probamos un candidato a divisor tenemos que hacer una división y es algo que cuesta tiempo, podemos considerar el número de divisiones como una medida del tiempo que tardamos.

Si tenemos que probar si cada número entre $1$ y $N$ es primo, para cada uno tenemos que hacer, en el peor caso (esto es, cuando sea primo), $K-1$ divisiones. Como esto lo hacemos para $K=1,2,3,\dots,N-1,N;$ podemos acotar superiormente el número de divisiones por:

\[(1-1)+(2-1)+\dots+((N-1)-1)+(N-1) \ = \ 1+2+\dots+(N-2)+(N-1)\]

Veremos a continuación cómo calcular una expresión cerrada de esta suma para poder hacernos una idea de cómo crece esto con $N$.

Proposición: $\ 1+2+3+\dots+N = N(N+1)/2$
Demostración: Sumamos dos veces la suma, una en orden inverso:

\[\begin{align*} &1&&+&&2&&+&&3&&+&&\dots&&+&&(N-1)&&+&&N \\ +\hspace{1em}&N&&+&&(N-1)&&+&&(N-2)&&+&&\dots&&+&&2&&+&&1 \end{align*}\]

Si nos fijamos, todas las columnas suman $N+1$, y tenemos $N$ columnas, por lo que en total tenemos $N(N+1).$ Como hemos sumado dos veces lo que queríamos, tenemos que dividir entre dos para recuperar la suma original, y tenemos nuestro resultado: $\ 1+2+3+\dots+N =$ $N(N+1)/2$ $\hspace{1em} \blacksquare$

Aplicando esta fórmula a la cantidad de divisiones que hacemos al buscar primos, tenemos que:

\[1+2+\dots+(N-2)+(N-1) = (N-1)N/2\]

Si por ejemplo quisiéramos buscar primos hasta $N=100,$ tendríamos un problema para hacerlo a mano, ya que se nos va a unas $5000$ divisiones. Si hacemos una división cada 5 segundos, podríamos llegar a tardar $7$ horas en hacer estos cálculos.

Es por esto que ya alrededor del 200 a.C., Eratóstenes se hizo la pregunta de si había alguna manera más eficiente de buscar números primos, y consiguió dar con un método mucho más eficaz.

La Criba de Eratóstenes

Dado un número, tratar de adivinar sus divisores resulta un problema extremadamente complicado. De hecho hoy en día no se conocen métodos eficientes para encontrar divisores de números grandes, y en parte la criptografía que nos protege diariamente en internet se basa en esta dificultad para factorizar números.

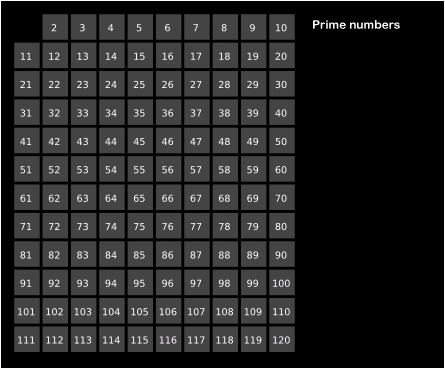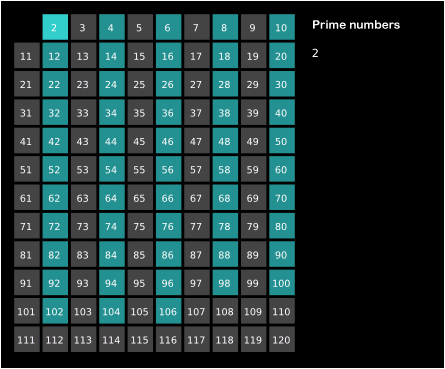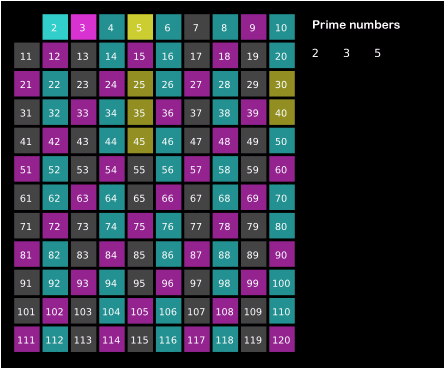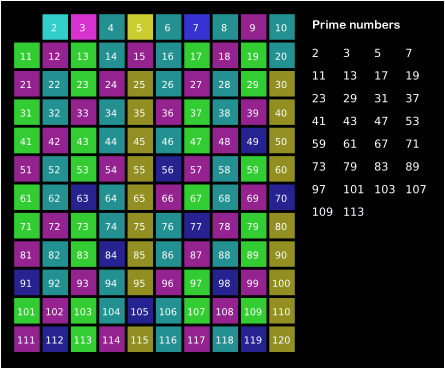
Sin embargo, si queremos buscar todos los primos entre $1$ y $N$, no tenemos por qué considerar cada número por separado. Esta idea permitió a Eratóstenes hacer un interesante descubrimiento: La idea es que lo haremos al revés, en lugar de buscar divisores para cada uno de los números, nosotros tendremos todos los números, y para cada uno descartaremos sus múltiplos, ya que estos seguro que no son primos, pero encontrarlos es inmediato.

Por ejemplo, el $2$ es primo, y podemos descartar sus múltiplos $4,6,8,10,\dots$ Luego encontraríamos el $3$ y como no era múltiplo de ningún número anterior, debe ser primo. Descartamos ahora sus múltiplos $6,9,12,15,\dots$ Como el $4$ había sido descartado como múltiplo de $2$, pasamos al siguiente primo, $5$, y así sucesivamente.

Este método se conoce como la Criba de Eratóstenes y resulta intuitivo al visualizarlo:

Cómo de eficiente es este método? En primer lugar en este método no se hacen divisiones, de hecho no es necesario ni hacer multiplicaciones, se puede hacer sumando. Aunque sumar resultará más sencillo que dividir, vamos a contar las sumas por igual que las divisiones en el anterior método.

Para descartar los múltiplos de un número $K$, tenemos que mirar sus múltiplos hasta $N$, por lo que miramos $N/K$ valores. El número de operaciones se puede acotar por:

\[\frac{N}{2} + \frac{N}{3} + \dots + \frac{N}{N-1} + \frac{N}{N} = N \left( \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{N-1} + \frac{1}{N} \right)\]

Si añadimos un $1$ al paréntesis, tenemos $1 + 1/2 + 1/3 + \dots + 1/N$, y resulta que esta suma es conocida como el $N$-ésimo número armónico, y se sabe que

\[\ \log N \le 1 + 1/2 + 1/3 + \dots + 1/N \le 1 + \log N,\]

por lo que podemos decir que como mucho este método hará $N \log N$ operaciones.

Nota 1: De hecho, solo hace falta descartar múltiplos de los primos, por lo que usando el teorema de los números primos se puede argumentar que, de hecho, este método hace en realidad $\sim N \log \log N$ operaciones, pero no es demasiado relevante para lo que trato de explicar ahora.

Nota 2: Usando integrales, puedes demostrar la cota de los números armónicos ya que:

\[1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{N} \le 1 + \int^{N}_{1} \frac{1}{x} dx = 1 + \log N\]

Si ahora queremos usar la Criba para $N = 100$, vemos que haríamos unas $460$ operaciones, lo que serían 40 minutos (criba) contra 7 horas (divisores), un $9.2\%$ del tiempo. Si aumentamos $N$ la diferencia se volverá más drástica. Con $N = 1000,$ hablamos de 9 horas (criba) contra $28$ días sin descanso (divisores).

Vemos aquí que pese a que el resultado sea el mismo, existen maneras más y menos eficientes de obtener los mismos resultados, y la diferencia de tiempo puede ser enorme, y para $N$ más grande crece esa diferencia. Es por esto que necesitamos una herramienta que nos permita comparar de manera más sencilla el número de operaciones que hace cada algoritmo.

Algoritmos

¿Qué es un algoritmo? Estos “métodos” que hemos discutido son ejemplos de algoritmos.
Un algoritmo es cualquier procedimiento secuencial, conjunto de reglas, etc… que resuelven un problema o hacen un cálculo.

El interés en los algoritmos, más allá de que sean correctos y calculen lo que se desea, está en el estudio de su eficiencia, y la comparación entre los algoritmos para un mismo problema, ya que en general encontrar un algoritmo muy poco eficiente es sencillo para la mayoría de problemas, suele consistir en general en probar todas las combinaciones hasta encontrar la correcta, o aplicar la definición del problema de la forma más simple posible, sin aprovechar posibles propiedades del problema.

Comportamiento asintótico

La idea es que como hemos visto, dos métodos completamente distintos no mantienen una relación constante de tiempo (el doble, el triple…), sino que en general crece la diferencia cuando crece $N$. Necesitamos una forma de catalogar en general los algoritmos en clases, independientemente de si uno hace unas pocas operaciones de más o menos, y centrarnos en esta parte tan importante que marca la evolución del tiempo necesario cuando crece $N$.

Con la aparición de los ordenadores, los casos donde $N$ es pequeña pierden bastante el interés ya que casi cualquier método es factible gracias a la velocidad de los ordenadores, y se vuelve mucho más importante el comportamiento cuando aumenta el valor de $N$. Para que os hagáis una idea, el caso $N = 1000$ anterior en el que estimábamos $28$ días de cálculos, un ordenador los haría en menos de una milésima de segundo. De hecho, por dar una referencia aproximada, un ordenador portátil promedio puede hacer alrededor de mil millones $(10^9)$ de operaciones básicas (suma, resta, multiplicación…) con números de tamaño razonable en un segundo.

Sigamos con la comparación de los dos métodos: por ejemplo, si llamamos $T_{\text{criba}}$ y $T_{divs}$ a los tiempos de los respectivos métodos, antes teníamos $T_{\text{criba}} = N \log N$ contra $T_{divs} = N(N-1)/2$. Haciendo las gráficas de estas funciones vemos la evolución con el aumento de $N:$

La clave es que si hacemos el ratio de tiempo $T_{\text{criba}}/T_{divs}$, tenemos que:

\[\frac{T_{\text{criba}}}{T_{divs}} = \frac{N \log N}{N(N-1)/2} = \frac{2 \log N}{N-1}\]

Vemos que esto tiende a $0$ rápidamente cuando $N$ crece. Esto significa que cuanto más grande sea $N$ la Criba se irá haciendo más y más eficiente respecto al método de los divisores. La otra idea importante es que tampoco habría afectado mucho un cambio constante en los tiempos, por ejemplo, aunque hagamos la Criba $10$ veces más lenta y el método de divisores $10$ veces más rápido, igualmente tendremos un ratio $200 \log N/(N-1).$

Aunque para valores de $N < 2000$ sí que ha habido un cambio, ya que el ratio es mayor que $1$ y la Criba estaría siendo más lenta, a partir de $2000$ vuelve a ganar la Criba y el ratio acaba tendiendo a $0$ para $N$ grande.

El comportamiento de una función cuando $N$ crece, independientemente de las constantes y términos pequeños, es lo que llamamos comportamiento asintótico.

Notación asintótica

Para poder centrarnos en comparar y catalogar los algoritmos según cómo se comportan de manera asintótica, dejando de lado detalles menos relevantes como constantes y partes poco significativas del total de la función, se introdujo el uso de la notación asintótica (o notación de Landau, o Big O). La idea es expresar la función separando términos y dejando solo los que tienen más peso, ignorando también las constantes.

Definición: Diremos que una función $f(N)$ pertenece a la familia $\mathcal{O}(g(N))$ si $f(N)/g(N) \to C \in \mathbb{R}$, es decir, que el ratio tienda a $0$ o a una constante, pero no que crezca hasta el infinito.
Intuitivamente es lógico. $\mathcal{O}(g(N))$ es la familia de funciones que como mucho crecen hasta una constante por $g(N)$, es decir, es una cota superior asintótica. Veamos un ejemplo:

Consideremos la familia $\mathcal{O}(N^2)$. Las funciones $3,$ $N,$ $100N^2,$ $N(N-1)/2,$ $N^2 + 1000N\log N$ todas pertenecen a esta familia. Puedes comprobarlo haciendo el ratio y viendo que tiende a alguna constante.
Sin embargo, $N^3, e^N, N^2 \log N, N!$ no pertenecen a esta familia. Diremos que son “más grandes”.

Por economizar, si $f(x)$ es de la familia $\mathcal{O}(g(N))$, diremos que $f(x) = \mathcal{O}(g(N))$. Con esto podemos decir, por ejemplo, que el método de los divisores para encontrar primos usaba $N(N-1)/2 = \mathcal{O}(N^2)$ operaciones. Por otra parte la Criba era $\mathcal{O}(N \log N)$, y al ver las funciones representadas por su versión más simple se puede ver casi a ojo que $T_{\text{criba}} = \mathcal{O}(N \log N)$ $< \mathcal{O}(N^2) = T_{\text{divs}}.$

Si igualamos dos familias, quiere decir que forman parte las mismas funciones.
Por ejemplo, un resultado conocido (referenciado más abajo) es que $\mathcal{O}(\log N!) = \mathcal{O}(N \log N)$. Hay que tener en cuenta que no hay una más pequeña que la otra, como sí puede pasar entre funciones en una misma familia.

Podemos calcular el coste asintótico operando con esta notación de forma natural:

Suma: $\mathcal{O}(f(N)) + \mathcal{O}(g(N)) =$ $\mathcal{O}(f(N) + g(N)) =$ $\mathcal{O}(\max\{f(N), g(N)\}).$
por ejemplo, si hacemos algo $\mathcal{O}(N^2)$ y luego algo $\mathcal{O}(e^N)$, tenemos un total de $\mathcal{O}(e^N) + \mathcal{O}(N^2) =$ $\mathcal{O}(e^N + N^2) =$ $\mathcal{O}(e^N)$.
Producto: $\mathcal{O}(f(N)) \times \mathcal{O}(g(N)) =$ $\mathcal{O}(f(N) \times g(N)).$
Por ejemplo, si hacemos $\mathcal{O}(N)$ veces algo que cuesta $\mathcal{O}(\log N)$, tenemos un total de $\mathcal{O}(N)\mathcal{O}(\log N) =$ $\mathcal{O}(N \log N)$.

El mejor algoritmo

Entonces, ¿cómo podemos saber si ya tenemos el mejor algoritmo o si aún existe alguno más eficiente?
Pues resulta que esta pregunta es muy complicada en la mayoría de casos.

Por ejemplo, por sorprendente que parezca, para el problema de encontrar primos existen algoritmos $\mathcal{O}(\frac{N}{\log \log N})$, es decir, ¡más rápidos que $\mathcal{O}(N)$!

La distribución de los números primos es complicada y desconozco si existe una cota mínima ajustada para la complejidad de encontrar los números primos menores que $N$. Lo que podemos saber es que por el Teorema de los números primos hay $\mathcal{O}(\frac{N}{\log N})$ primos, por lo que no se puede hacer más rápido que esto, y estos últimos algoritmos mencionados están cerca de este límite.

Próximamente hablaremos de casos en los que sí podemos decir que tenemos el mejor algoritmo, aunque no sea, desgraciadamente, el caso habitual.

Extra: Algunos resultados importantes

Números armónicos:

\[H_N := 1+ \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{N-1} + \frac{1}{N} = \mathcal{O}(\log N)\]

Suma de los inversos de los primos:
La suma de los inversos de los primos hasta $N$ ($P \le N$) es:

\[\frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \dots + \frac{1}{P} = \mathcal{O}(\log \log N)\]

Logaritmo del factorial (Stirling):
$\mathcal{O}(\log N!) = \mathcal{O}(N \log N).$
Teorema de los números primos:
La cantidad de números primos entre $1$ y $N$ es $\mathcal{O}(\frac{N}{\log N}).$
Suma de divisores:
La suma de los divisores de cualquier entero $N$ es $\mathcal{O}(N \log \log N).$
Número de divisores:
Para cualquier $\varepsilon > 0$, $N$ tiene $\mathcal{O}(N^\varepsilon)$ divisores.
En programación competitiva resulta razonable pensar en $\varepsilon = 1/3.$

Extra: Ejemplos prácticos con código

1
2
3
for i = 1..N:
    for j = 1..N:
       ... # operaciones básicas

Un código de esta forma haría $\mathcal{O}(N^2)$ operaciones.

1
2
3
for i = 1..N:
    for j = 1..N/i:
       ... # operaciones básicas

Este código es similar al de la Criba, haría $N + N/2 + N/3 + \dots = \mathcal{O}(N \log N)$ pasos.

1
2
3
4
5
for i = 1..N
    j = 1
    while j*j <= N:
        ... # operaciones básicas
        j += 1

Este código se ejecuta para cada $i$ mientras $j^2 \le i$, es decir, mientras $j \le \sqrt{i}$, por lo que hará $\sqrt{1} + \sqrt{2} + \dots + \sqrt{N} = \mathcal{O}(N \sqrt{N})$ operaciones.

1
2
3
4
5
for i = 1..N
    j = 1
    while j <= i:
        ... # operaciones básicas
        j += j

Este código se ejecuta para cada $i$ mientras $j \le i$, pero a cada paso $j$ se duplica, por lo que el bucle interno hará $\log_2(i)$ operaciones. Esto es un total de $\log_2 1 + \log_2 2 + \dots + \log_2 N = \mathcal{O}(N \log N)$ operaciones.

1
2
3
4
5
6
7
8
l = 1
r = N+1
while r - l > 1:
    m = (l + r) // 2
    if m*m <= N:
        l = m
    else:
        r = m

Este codigo mantiene un intervalo $[l, r)$ duante su ejecución. A cada paso, $m$ es el punto medio y luego, dependiendo de la condición, modifica $l$ o $r$, quedando un intervalo de la mitad de tamaño. Esto pasa hasta que el intervalo tenga longitud menor a $2$. Cada paso divide entre dos la longitud, por lo que es $\mathcal{O}(\log N)$.
¿Sabes qué calcula?